Semantic-Geometric Planning

Even when rich domain specific knowledge is available, designing a good heuristic function can be difficult, which maps such the knowledge to the right cost-to-go value. Consider for example, driving a car in an outdoor environment, where there are road and grass. Heuristically, we know that driving on road is better than driving on grass but finding a function that encodes such the heuristic is not trivial so to prioritize the paths on the road over the paths on the grass. In another example, consider driving a car to a destination using a GPS navigator, where the navigator computes some high-level paths, or waypoints, and the driver computes some low-level dynamically feasible paths following the waypoints. In the low-level planning, finding a numerical function that maps the path to the right cost-to-go is not trivial so to prioritize the paths staying close to the waypoints over the other paths.
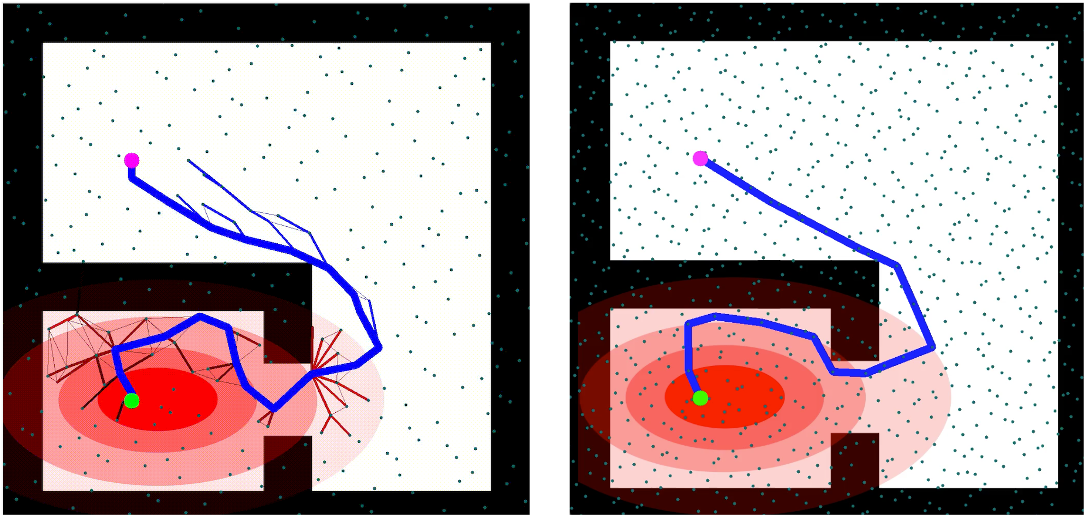
We leverage colored planning framework which utilizes semantic heuristics for guiding the search in a principled way. We first encode the semantic and geometric information on a weighted colored graph, in which an edge weight function maps each edge to a non-negative value and the edge set is partitioned into a finite set of colors with ranks. Using a weighted colored graph we represent the semantic information with color and the geometric information with weight. We define the optimal path on a weighted colored graph as the shortest path with minimal inclusion of low-ranked colored edges. We then propose a class of algorithms which perform an A*-like search on weighted colored graphs to produce the optimal path. The proposed framework allows a more direct exploitation of a richer representation of the environment, namely, a joint semantic and geometric abstraction of the environment.
Publications
Class-Ordered LPA*: An Incremental-Search Algorithm for Weighted Colored Graphs
Lim, J., Salzman, O., and P. Tsiotras, “Class-Ordered LPA*: An Incremental-Search Algorithm for Weighted Colored Graphs,” in 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 6907-6913.
A Generalized A* Algorithm for Finding Globally Optimal Paths in Weighted Colored Graphs
Lim, J., and Tsiotras, P., “A generalized A* algorithm for finding globally optimal paths in weighted colored graphs,” in 2021 IEEE International Conference on Robotics and Automation (ICRA), pp. 7503–7509.
